Historical Fatal and Non-fatal Nuclear Fission Criticality Accidents; Preventing Them in Aqueous Solutions of Plutonium.

[NNadir]

The paper to which I'll refer in this post is this one: A Semi-Empirical Density Law for Ternary, Homogeneous PuCl3/HCl/H2O Solutions Kelly E. Aldrich, Kimberly B. Muscarella, Justin N. Cross, Natalie T. Rice, Dung M. Vu, Christopher J. Godt, Riley Bulso, Stephen K. Cope, David J. Kunsberg, John H. Matonic, David B. Kimball, Jennifer L. Alwin, Theresa E. Cutler, and James Bunsen Industrial & Engineering Chemistry Research 2025 64 (9), 4736-4748.

The full paper is free to read on line at the link if one is interested in doing so. Nonetheless, I'll excerpt it and remark on reference 1, which is also publicly available for free reading and download, and lists accidents in which fissionable nuclear materials went, unexpectedly, into critical chain reactions in American, Soviet, and Japanese facilities, some of which were weapon facilities.

The introductory text:

Working with fissile material poses several unique challenges only encountered within the nuclear industry. One of the primary hazards unique to handling fissile isotopes, such as ²³⁵U or ²³⁹Pu, is the risk of a criticality accident. A nuclear criticality accident occurs when the same chain reaction that can be used to productively generate electricity in a nuclear reactor─a self-sustaining chain reaction of nuclear fission─occurs in an uncontrolled manner. When this occurs, nearby people, structures, and containment systems are exposed to a massive burst of damaging energy in the form of radiation (neutron and gamma) and heat. Often these accidents are fatal and/or result in the destruction of facilities or release of material to the environment. (1)

Part of the challenge in guarding against a nuclear criticality accident is the time scale. There are no advanced indications or warnings of an impending criticality, and the instantaneous nature with which a system can shift from subcritical to critical or supercritical leaves no window of time for corrective measures. This equates to a single viable safety approach for dealing with potential criticality accidents: prevention. (2−4)

Accident prevention relies heavily on advanced neutron transport modeling, conducted with Monte Carlo simulations using programs such as the MCNP code, SCALE, CRISTAL, etc. (5−8) To apply simulations that facilitate the design of safe systems and operations, critical safety analysts first build a detailed model of the operation being performed. This construct has many parameters that must be defined, including details such as isotopic composition, fissile mass, shape, density, elemental composition, and concentration, in addition to the environmental descriptions of process equipment that interacts with the material. The model is then used to simulate neutron transport (propagation) through the system and determine the neutron multiplication or k_eff . (2) Typically, this analysis is performed iteratively across a range of conditions that represent normal operation as well as credible abnormal conditions or deviations from the planned process that may be encountered. The outputs of these calculations are compiled to define the limits of an operation that will prevent the system from reaching a critical (k_eff = 1) or supercritical state (k_eff greater than or equal to 1). (1−4)

While it is a crucially important component of nuclear criticality safety, this modeling approach has significant limitations. Namely, the accuracy of the simulated k_eff output is heavily affected by the accuracy of the model input. Thus, small errors in assumed parameters used in the model propagate. Inaccurate assumptions in solution system models often come from a lack of experimental data describing the system. While the elemental composition can be described with relative accuracy (using atomic or weight %), the density of the system is typically fictitious, derived from the additive volumes and masses of the components based on wt %. Of course, this approach ignores the nuanced and significant impacts of ionic strength, coordination environment, hydrogen bonding, etc., that contribute to the true density of a solution.

It has been previously demonstrated in aqueous actinide nitrate systems that the models built to estimate a solution system may be significantly inaccurate compared to the output when experimental density values are used in modeling. Specifically, the derivation of a plutonium nitrate density law, and subsequent implementation of that density law in CRISTAL/SCALE calculations, identified an underestimation of k_eff by a small margin (∼0.03), which meant that scenarios thought to be below the safety margin (upper subcritical limit) were actually slightly above it. (9−12) This example shows the potential for bias and error when using assumed or estimated solution characteristics compared to experimentally determined characteristics.

Development of an analogous density law describing actinide chloride salts in aqueous chloride matrixes has not yet been established. (13,14) While in aqueous chloride systems it is generally accepted that modeling assumptions result in exceedingly conservative evaluations (particularly because chloride concentration is not credited and the ³⁵Cl(n,gamma) reaction is a significant thermal neutron absorber) (15−17) this work with nitrate exemplifies the cautionary lesson of proceeding without accurate parameters on which these calculations and resulting operational restrictions are based. (11,12)

k_eff can be thought of as the probability that the neutrons released in a nuclear fission will result in the fission of another atom. Generally a fissioning atom will release more than one neutron, the number being an important parameter in nuclear engineering usually designated with the greek letter "eta" which varies with the nature of the atom (almost always an actinide) as well as the energy of the neutron causing the fission. I have been known to incorrectly refer to k_eff as "reactivity" which is actually the ratio: k_eff-1/k_eff, not k_eff itself. If k_eff is equal to one, the nuclear system is critical and will operate at constant power, as in an operating nuclear power reactor. The reactivity is zero. If it is less than one, the power will decrease and ultimately stop (for fission but not for decay products) or will not start in the first place. It is said to be "sub-critical" and the chain reaction will terminate, although spontaneous fission events will still take place. The reactivity is negative. If it is more than 1, the reactivity is positive and the power will increase. In the Manhattan Project, with its somewhat quaint reliance on code terms, the unit of reactivity, which is a percentage, as "cents" and "dollars," a coinage, excuse the pun, attributed to Louis Slotin, a Canadian physicist, who has it happens was one of the few people who actually was trained to assemble a nuclear weapon, and, who, regrettably, was one of the first people to be killed by a criticality accident when he accidentally let a plutonium hemisphere drop on to another hemisphere that he was holding apart with a screwdriver.

The "dollars" and "cents" nomenclature has now been replaced by "pcm" percent mille, one thousandth of a percent for power reactors, for nuclear weapons, the reactivity has to be very high, dollars, since the idea is to fission as many atoms as possible as quickly as possible.

The value of k_eff is determined by a number of factors, for instance the presence of atoms that absorb neutrons but do not fission (as in control rods), the average energy of the neutrons in the flux, and the probability that a neutron will be slowed by collisions or remain at the energy at which they were released - in nuclear fission this energy is generally around 1 to 2 MeV (million electron volts), in most nuclear reactors they are slowed, "thermalized" to a value taken to be 0.0253 eV which is close to the average energy of atoms at room temperature. The shape of the container in which the fuel is contained is a very important property for determining k_eff, as well as the nature of the surroundings. This is generally a geometrical term that reflects how far neutrons must travel before they "leak" out of the system. If they leak, they will not cause a fission unless reflected back into the container. Human flesh acts as a neutron reflector (as do other materials) and can effect k_eff. People have been killed or injured as a result of acting as neutron reflectors near otherwise subcritical masses. The geometry of the container, usually represented by the formulas for shape and volume, is known in nuclear engineering as "buckling" and depending on geometry, can appeal to ordinary 3D vector calculus.

Anyway. Reference 1: A Review of Criticality Accidents (2000)

Now let's turn to reference one: which is this one, a list of American, Soviet era, and Japanese events where fissionable materials

Here's a graphic showing the 22 cases of such process accidents, which involves weapons facilities but not accidents involving the assembly of weapons themselves, Louis Slotin's death is omitted.



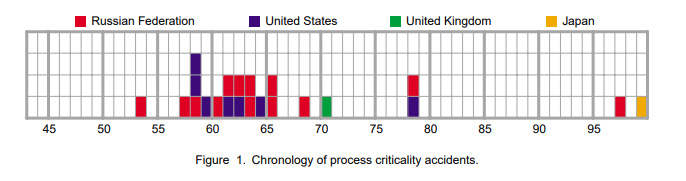
Each accident is described in detail, with a heading for the number of people who were seriously or significantly exposed or died.

Totaling these, I find 7 "serious exposures," 30 "significant exposures, and 9 deaths over a period of half a century.

Why am I, an advocate for nuclear energy telling you this?

Nuclear energy is not risk free, but then again, the question that is never raised is "does it have to be risk free to be better than everything else?"

How one answers this question is a reflection, in my view, of one's ability to think critically or, for that matter, how to think ethically.

Every year, about 7 million people die from combustion waste, aka air pollution. People can hold forth endlessly about Fukushima or Chernobyl or even more insipidly, Three Mile Island, but they just don't give a rat's ass how many people fossil fuels kill every damned day, about 19,000 people.

The Piper Alpha oil platform explosion in 1988 killed 168 people in a few hours, but people don't really complain about the use of fossil fuels except in the abstract. The Deepwater Horizon disaster killed 11 people, two more than have died from reported nuclear criticality accidents in the last century, and the health effects of exposure to crude oil are not measured but surely not significant.

Of course, Piper Alpha and even Deepwater Horizon have both gone down the Orwellian memory hole, and that, the selective attention, as much as anything else, is why the planetary atmosphere is collapsing.

Have a nice evening.